連載　オブジェクト指向と哲学
第34回　集合と写像

　前回迄「鶏と卵」と題して自己生成モデルについて考えてきました。このテーマは一旦置いておき、今回は話題を変えて、オブジェクト指向の基礎となる「クラスとインスタンス」および「クラス間の関連」を、数学の基礎となる「集合と写像」との対応関係で考えてみたいと思います。

■クラスのインスタンスは集合の要素
　クラスはオブジェクトの集合と捉えることができます。集合としてみればインスタンスは集合の要素です。

　　　　xはクラスXのインスタンス　⇔　xは集合Xの要素

　これを記号で表すなら次の図1のようになります。

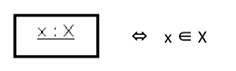
　　　　図1　インスタンスと要素

■関連と写像
　２つのクラスXとYの間にfという関連があるとします。XからYへ誘導可能とし、Y側の多重度は1とします。X側の多重度は任意です（図2）。

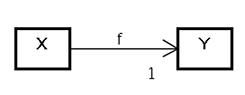
　　　　図2　関連のモデル

　このときXの任意のインスタンスxに対してxとリンクするYのインスタンスyが必ず存在し、yは一意です。

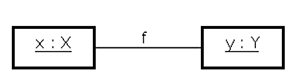
　　　　図3　任意のxとリンクするyは一意に存在する

　集合と写像で考えるなら、fは集合XからYへの写像です。つまり図2のクラス図から

　　　　∀x∈Xに対して∃1 y∈Y : y = f(x)

となります。Y側の多重度は丁度1でなければ写像としては定義できません。従って以上をまとめると、クラス間の関連と集合間の写像の関係は次の図4のようになります。

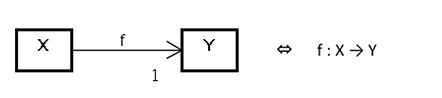
　　　　図4　関連と写像の関係

■多重度と写像の関係
　次はX側の多重度と写像の関係を考えます。関連の多重度は写像として全射／単射／全単射の違いと関係します。

■全射onto (surjection)
　X側の多重度を1以上とします。図5のように1..*でも単に2でもかまいません。このとき写像f : X→Yは全射となります。つまりクラス図のX側の多重度>0なので
　　　　∀y∈Yに対して∃x∈X : y = f(x)
となり、図5の関係が成立します。

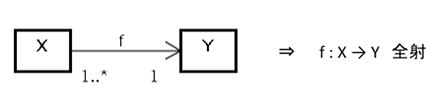
　　　　図5　全射の例

　逆は、全射であるためには
　　　　∀y∈Yに対して∃x∈X : y = f(x)
となるインスタンスxが存在すればよいので、クラスX側の多重度>0であれば条件が満たされます。まとめると図6の関係が成立します。

　　　　
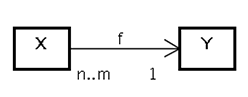
　　　　n>0かつ（m≧nまたはm=*）⇔　f : X → Y は全射

　　　　図6　多重度と全射の関係

■単射one to one (injection)
　X側の多重度を0..1とします。このとき写像f : X→Yは単射となります。つまりクラス図から
　　　　x0∈X, x1∈X, x0≠x1　⇒　f(x0) ≠ f(x1)
となります。
　逆に単射なら、もしもX側の多重度>1ならばクラスXのふたつのインスタンスx1とx2が Yのひとつのインスタンスとリンクすることもあるのでf(x1)=f(x2)となりfが単射である前提に矛盾します。

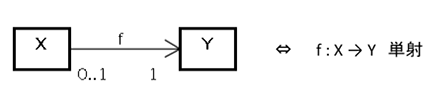
　　　　図7　多重度と単射の関係

■全単射one to one, onto (bijection)
　X側の多重度も丁度1ならば写像f : X→Yは全単射です。

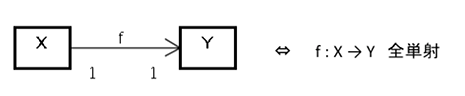
　　　　図8　多重度と全単射の関係

→方向の証明
　　　　∀y∈Yに対して∃x∈X : y = f(x) ∴fは全射
　　　　x0∈X, x1∈X, x0≠x1　⇒　f(x0) ≠ f(x1) ∴fは単射

←方向の証明
　　　　fは全射なのでX側の多重度>0
　　　　fは単射なのでX側の多重度≦1
　　　　∴X側の多重度=1

（以下次回）

【参考書籍】
[1]瀬山士郎「なっとくする集合／位相」講談社、2001

ODL Object Design Laboratory, Inc. Akio Kawai