連載 オブジェクト指向と哲学
第36回 集合と写像(3)− 集合と要素はどちらが先か?
当連載「集合と写像」編では、これまでクラスを単なる集合として扱い、特に属性や操作は考えていません。本来、集合をクラスと考えるためには、集合の要素に属性と操作を定義しなければ意味がありません。クラスと考えることによるメリットは、集合のベン図に替えてUMLのクラス図やオブジェクト図を使用することができることです。
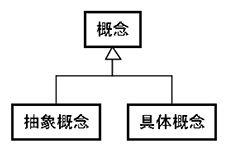
集合とその要素は、抽象概念と具体概念と考えることができます。抽象概念をクラスとし、具体概念をインスタンスと呼んでいます。今回これらの類似した意味を持つ用語「集合、クラス、概念」を一度整理してみたいと思います。
■カントルの集合
集合という概念を数学として初めて定式化したカントルは、超限集合論[1]で集合を次のように定義しています。
--
集合なる述語によって、われわれはいかなる物であれ、われわれの思惟または直観の対象であり、十分に確定され、かつたがいに区別される物 m(これらの物はこの集合の要素と名づけられる) の、全体への総括 M を言うと理解する。
記号としては、われわれはこれを次のように表す:
M = { m }
--
集合Mを定義する前にまず何らかのものmの存在が前提です。その集まりが集合ですが、全体への総括という言葉で表現されています。集合より要素の存在が優先します。
■オブジェクト
ランボーのUMLリファレンスマニュアル[2]には、カントルの集合のmに対応するオブジェクトは次のように説明されています。
--
オブジェクト(object):
はっきり定義された境界とアイデンティティを持つ個別の実体。状態と振る舞いがカプセル化されている。クラスのインスタンス。[2]
--
次に集合Mに対応するクラスは
--
クラス(class):
同一の属性、操作、メソッド、関係、および振る舞いを共有しているオブジェクトの集合に対する記述子。 [2]
--
単に集合ではなくその記述子だと説明されています。クラスよりもオブジェクトの存在が優先します。
--
記述子(descriptor):
一群のインスタンスの共通のプロパティ、たとえば、それらの構造、関係、振る舞い、制約、目的などを記述するモデル要素。[2]
--
つまりクラスとは「インスタンスの集合を記述するモデル要素」[2]です。これはカントルの集合とは「mの全体への総括 M」という定義と似ています。
■概念とは
ところで集合の定義は概念の定義にも似ています。広辞苑から引用します。
--
概念(concept):
事物の本質をとらえる思考の形式。事物の本質的な特徴とそれらの連関が概念の内容(内包)。概念は同一本質もつ一定範囲の事物(外延)に適用されるから一般性をもつ。
--
概念はカントルのMに、外延がmに対応します。概念はクラスに、外延がオブジェクトに対応します。
次に概念と抽象概念はどう違うのか?
--
抽象概念(abstract concept):
具体的な個物ではなく、その個物に属しはするが、それから分離して考えられうる性質や関係を指す概念。
--
概念と抽象概念は同じようです。抽象概念の説明に概念を用いていますが、概念の意味をはっきりさせないとこの説明は意味がありません。
この説明は、抽象概念は概念の一種、「抽象概念is-a 概念」と読みとることができます。ならば抽象概念でない概念もありそうです。
抽象概念に対して具体概念が説明されています。
--
具体概念
事物のあらゆる面、他物との関連を明らかにして事物を全面的にとらえる概念。⇔抽象概念。
--
この説明の概念は本来の概念とは異なります。本来の概念は抽象概念と同じ扱いで具体的なものを示すものではありません。
つまり概念には抽象概念と具体概念があり、単に概念(広辞苑の項目)と言った場合は抽象概念を示すということのようです。
「抽象概念is-a 概念」でありt「具体概念is-a 概念」なので2種類の概念があることになり、広辞苑の項目の概念(=抽象概念)と図1の概念(広義の概念)は異なります。
次に明鏡国語辞典を見てみます。
--
概念:
個々の事物から共通する性質を抜き出し、それらを総合して構成する普遍的な表象。言語によって表され、内包と外延をもつ。
--
広辞苑では思考形式と表現されていますが、明鏡では表象ということばで表現されています。
--
表象:
哲学・心理学で、知覚に基づいて心に思い浮かべる外界の対象の像(イメージ)。
--
概念を思考形式と言ったり、イメージと言ったり、クラスは集合に対する記述子、集合は全体への総括であるなど直感的に理解し難い表現が用いられていますが、言いたいことは同じようです。
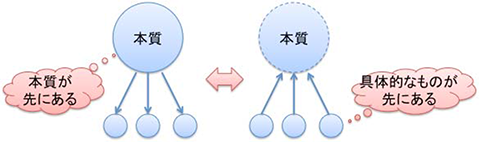
ところでこの2つの辞書の説明には大きな違いがあります。明鏡は、まず具体的な事物があってそれらの共通点を総合したイメージを概念だとしています。これはカントルの集合の定義と同じです。カントルはmが先にあってその総括をMとしています。オブジェクトがあってクラスがあるのと同じです。
一方広辞苑は、具体的なものの共通点を引き出すとは言わず、ただ本質を捉えるとしています。対象がひとつでもよさそうです。結果的に具体的な外延に適用される。カントルの定義に当てはめるなら、まずMを定義し、そこにmを追加することになり、順序が逆です。
オブジェクト指向プログラミング言語JavaやC++では先にクラスを定義し、実行時にオブジェクトを生成しますが、それは実装技術レベルのことであり、考え方としてはオブジェクトの存在がクラスの存在に優先します。オブジェクトが存在するからクラスを記述できるわけです。
■本質は先にあるのか後付けか?
本質と呼ばれるものはどこにも存在せず、人が複数の具体的なものから引き出した共通点を単に本質と呼んでいるにすぎないのか、それとも本質というものが存在して、それが具体的なものの中に埋め込まれており、それを人が発見するのかという哲学的な議論があります。
議論は本質というものの存在の有無と、存在するならそれはどこにあるのか、つまり3つに分類できます。
(1)本質は存在しない。人が共通点を単にそう呼ぶだけのこと。
(2)本質は個々のものに埋め込まれていて取り出せない(アリストテレス説)
(3)本質はイデアとして別世界に存在する(プラトン説)
■プラトンvs.アリストテレス
またしてもイデアが先に存在するのか、それは具体的なものの後付けかという議論に戻ります。アリストテレスは「本質=形相」は存在するが個々の物の中に埋め込まれていて取り出せないとしています。
次回はクラスの属性について考えてみたいと思います。
【参考書籍】
[1] カントル G.Cantor、【訳】功力金二郎、村田全「超限集合論」、共立出版、1979
[2] J.ランボー、I.ヤコブソン、G.ブーチ、【監訳】石塚圭樹「UMLリファレンスマニュアル」、ピアソン/エデュケーション、2002
ODL Object Design Laboratory, Inc. Akio Kawai