連載　オブジェクト指向と哲学
第35回　集合と写像（２）− 関連と関連クラス

　前回は、オブジェクト指向の基礎となる「クラスとインスタンス」および「クラス間の関連」を、数学の基礎となる「集合と写像」と対比して考えました。
　クラス間の関連は集合間の写像に対応し、関連の多重度は写像の単射／全射／全単射と対応することを示しました。
　今回は関連と関連クラスについて、集合と写像の観点から整理します。

■集合間のマッピング
　２つの集合の要素間の何らかの意味的な関係をマッピングと呼ぶことにします。
例えば図1は集合XとYのマッピングを、要素間を線で接続することで表しています。この関係は必ずしも1対1とは限りません。

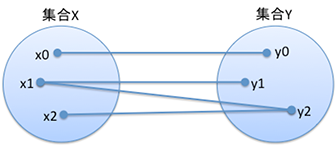
　集合間のマッピングは要素のタプルで表すことができます。図1なら(x0, y0) 、(x1, y1)、 (x1, y2) および(x2, y2)の４つのタプルで表すことができます。

■リンクとは
　オブジェクト指向用語のリンクとは、オブジェクト参照のタプルです。
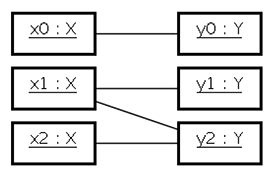
クラスXのインスタンスxとクラスYのインスタンスyのリンクは、xとyのタプル (x, y) で表すことができます。UMLで次のように記述します。

　図１のXとYをクラスと考えるなら、集合としての要素間のマッピングはオブジェクト間のリンクとして図３のように表すことができます。

■関係を集合と考える
　図１の集合間のマッピングもまたひとつの集合と考えることができます。XとYのマッピングを表す４つのタプルからなる集合をRとします。図１は集合として次のように表すことができます。
　　　　X = {x0, x1, x2}
　　　　Y = {y0, y1, y2}
　　　　R = {(x0,y0), (x1,y1), (x1,y2), (x2,y2)}

■関連とは
　集合Rをクラスと考えます。集合をクラスと呼ぶ以上ある条件を満たしている必要がありますが、それは今は置いておきます。

　UMLではクラス間の関連とはインスタンス間のリンクを意味します。個々のインスタンス間のリンクを抽象化したものがクラス間の関連です。UMLではクラス間を線で結んで関連を表します。例えば図４はクラスXとYの関連を表します。

　図３の４つのリンクがここに含まれます。

■関連クラスとは
　関連はリンクの集合としてクラスと考えることができるなら、UMLでは矩形で表すこともできる筈です。この関連とクラスという２つの意味をもつUMLの要素を関連クラスと呼び、図５のように表します。

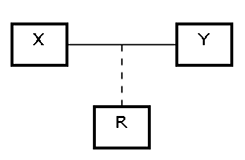
　関連クラスRのインスタンスはXとYのインスタンスを決めれば一意に決まります。

■関連クラスと写像
　集合と写像で考えるならXとYの直積X×YからRへの写像fを
　　　　f : X × Y → R
　　　　x∈X, y∈Yに対してf(x, y) = (x, y)∈R
と定義することができます。

　この写像fは全単射です。

全射

単射

（以下次回）

【参考書籍】
[1] 瀬山士郎「なっとくする集合／位相」講談社、2001
[2] J.Martin, J.Odell, “Object Oriented Methods − A Foundation”, Prentice Hall, 1998

ODL Object Design Laboratory, Inc. Akio Kawai